
لعبت خوارزميات البرمجة دورًا بالغ الأهمية في إنشاء وتشكيل المنصات من حولنا. تستخدم الخوارزميات عادة لبناء منصات متصلة بالإنترنت أو غير متصلة بالإنترنت تتطلب إجراء عملية حسابية محددة. والسبب وراء انتشار الخوارزميات واضح، إذ يمكنها حل جميع مشاكل البرمجيات، وتسهل على المطورين بشكل عام. في هذه المقالة، سنتعرف الخوارزميات في البرمجة، ونشرح أنواعها، ونعدد تطبيقاتها. لذا، ابقوا معنا حتى النهاية.
جدول المحتويات
ما هي خوارزميات البرمجة؟
خوارزميات البرمجة (Algorithms Programming) هي مجموعة من الخطوات المنطقية المنظمة التي تستخدم لحل مشكلة أو إنجاز مهمة محددة. تعمل الخوارزمية على تحويل البيانات المدخلة إلى نتائج أو مخرجات من خلال سلسلة من العمليات المعرفة بدقة.
كل خوارزمية تستقبل بيانات دخل، وتمر بخطوات محددة، لتنتج في النهاية خرجًا يمكن استخدامه في التطبيق أو التحليل.
تتفاوت الخوارزميات من حيث التعقيد، فهناك ما هو بسيط مثل: البحث عن كلمة ضمن قائمة كلمات قصيرة، وهناك ما هو معقد مثل: العثور على أقصر طريق بين نقطتين في شبكة طرق ضخمة تحتوي على آلاف الطرق.
عادةً ما تكتب الخوارزميات أولًا بصيغة الكود الزائف (Pseudo Code)، وهي طريقة تعبر عن فكرة الخوارزمية بلغة منطقية قريبة من لغات البرمجة ولكن غير مرتبطة بلغة برمجة محددة. فعلى سبيل المثال، يمكن كتابة خوارزمية البحث عن كلمة في قائمة بالشكل التالي:
- تجهيز قائمة من الكلمات
- تحديد الكلمة المراد البحث عنها
- البدء من أول القائمة
- مقارنة كل كلمة بالكلمة المطلوبة
- إذا وُجدت مطابقة، يتم إرجاع “موجودة”
- إذا انتهت القائمة دون العثور عليها، يتم إرجاع “غير موجودة”
إلى جانب الكود الزائف، تستخدم مخططات التدفق (Flow Charts) كوسيلة تصوّر مرئية لخطوات الخوارزمية، وتوضح تسلسل العمليات ونقاط اتخاذ القرار داخلها.
مع تطور التكنولوجيا واكتساب المشكلات تعقيدًا أكبر، أصبح تصميم خوارزميات فعالة وسريعة ضرورة ملحة. فمثلًا، إدارة حركة الطائرات في المطارات الكبرى، أو تحليل بيانات التسلسل الجيني البشري، أو تنظيم التفاعلات في شبكات التواصل الاجتماعي الضخمة تتطلب خوارزميات عالية الكفاءة. ولذلك، يركز المبرمجون والباحثون عند تصميم الخوارزميات على السرعة وكفاءة الاستخدام للموارد، خاصة عند التعامل مع كميات ضخمة من البيانات.
خصائص خوارزميات البرمجة
تتميز خوارزميات -على أساس بنائها- بخاصية الدقة كفكرة أساسية في تصميمها، وتظهر في تحديد الخطوات بدقة تامة، إلى جانب التفرد في إعطاء نتائج كل خطوة بشكل واضح ومحدد، بحيث تعتمد فقط على المدخلات ونتائج الخطوات السابقة. كما يجب أن تكون الخوارزمية منتهية، أي تصل إلى نتيجة بعد تنفيذ عدد محدود من الخطوات، لتجنب دخولها في حلقات لا نهائية (Infinite Loop).
وذلك بالإضافة إلى وجود عنصرين أساسيين في عملية التنفيذ: المدخلات (Input) والمخرجات (Output)، حيث تستقبل الخوارزمية البيانات وتنتج نتائج بعد المعالجة، مع ضمان قدرتها على التعامل مع مختلف حالات المدخلات ضمن نطاق معرف.
مميزات الخوارزمية البرمجية
- دقيقة: جميع المراحل مخطط لها بدقة تامة.
- متميزة (وحيدة): مفاهيم ونتائج كل مرحلة تعرَف بشكل فريد، وتعتمد فقط على المدخلات.
- منتهية: تتوقف الخوارزمية بعد تنفيذ عدد محدود من الأوامر.
- مدخلات: تستقبل الخوارزمية بيانات دخول (مدخلات).
- مخرجات: تنتج الخوارزمية نتائج بعد المعالجة.
فوائد الخوارزميات في البرمجة
- تقدم حلًا مرحليًا للمشكلة المطروحة، مما يسهل فهمها.
- تعتمد على عملية واضحة ومحددة للوصول إلى النتيجة.
- غير مربوطة بلغة برمجة معينة.
- لكل خطوة في الخوارزمية تسلسل منطقي واضح، مما يسهل عملية التصحيح (Debugging).
أنواع خوارزميات البرمجة
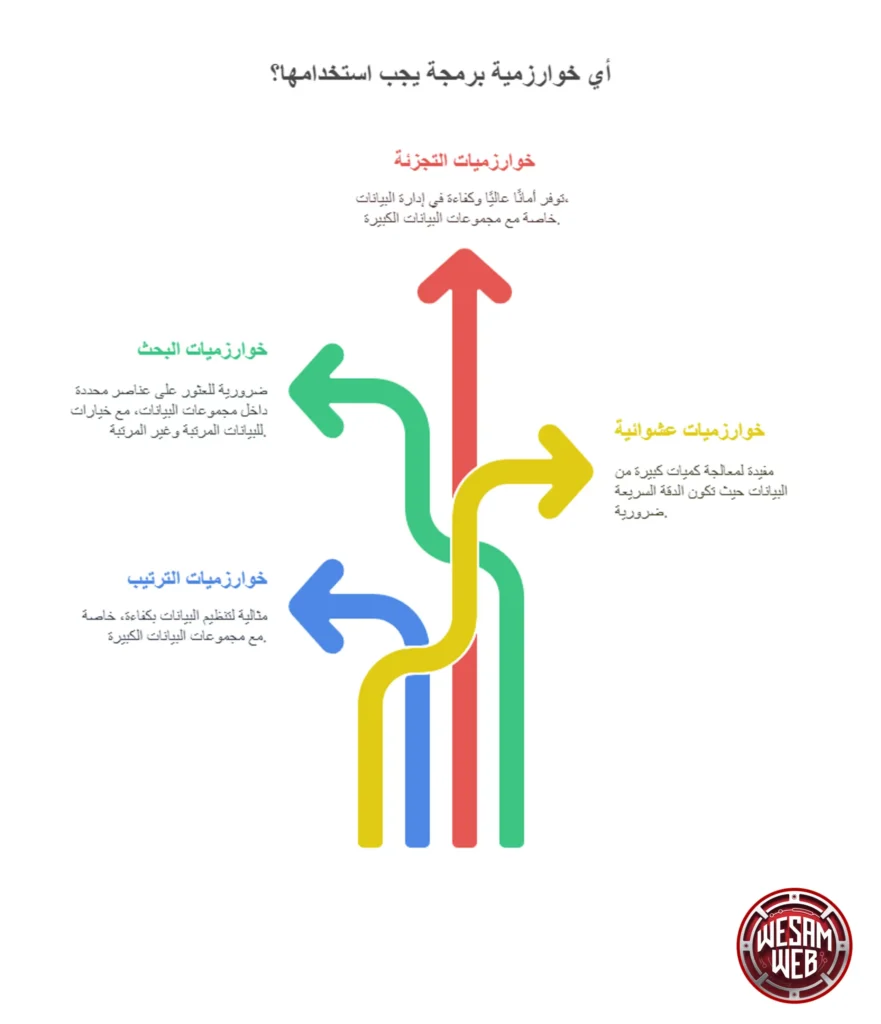
يوجد اليوم آلاف وملايين الخوارزميات المختلفة المستخدمة في البرمجة. ولذلك، إذا أراد مطورو البرامج وهندسة البرمجيات التقدم في هذا المجال واحترافه، يجب أن يكونوا على دراية بأنواعها المختلفة. بهذه الطريقة سيعرفون ما هي الخيارات المتاحة أمامهم، وفي أي وقت يكون استخدام كل خوارزمية مناسبًا.
يمكن للخوارزميات أن تعثر على أفضل وأكثر الطرق كفاءة لحل المشكلات. وبذلك لا تساعد فقط في زيادة السرعة، بل تستهلك أيضًا ذاكرة أقل من الحاسوب. فيما يلي قائمة بأهم وأشهر خوارزميات البرمجة المُستخدمة، مع شرح كل منها بشكل منفصل.
1. الخوارزميات الخاصة بالترتيب (Sorting Algorithms)
تعد عملية تنظيم البيانات الخام في علوم الحاسوب خطوة بسيطة ولكن ضرورية جدًا. خاصة في العصر الحالي الذي نتعامل فيه مع كميات هائلة من البيانات، حيث يتضاعف أهمية هذه الخطوة عدة مرات. يقصد بالترتيب عادة إيجاد ترتيب رقمي أو أبجدي تصاعدي أو تنازلي. فيما يلي أبرز أنواع خوارزميات الترتيب الشائعة:
الترتيب بالإدخال (Insertion Sort)
تعمل هذه الخوارزمية على ترتيب البيانات مرحلة بعد مرحلة وبالتوالي. بمعنى آخر، تقوم بفحص العناصر غير المرتبة وتضع كل عنصر في مكانه الصحيح المناسب. وبهذه الطريقة يتم الحصول على قائمة مرتبة تمامًا. غالبًا ما يستخدم مثال ترتيب بطاقات اللعب لتوضيح عمل هذه الخوارزمية.
على سبيل المثال، إذا أردنا ترتيب مجموعة من البطاقات، يمكننا تصنيف الأرقام من الأصغر إلى الأكبر في الجهة اليسرى، بينما نضع الشخصيات مثل الملك والملكة والفرس في الجهة اليمنى، حتى تصبح جميع البطاقات مرتبة من الأصغر إلى الأكبر. تستخدم هذه الخوارزمية بكثرة في التعامل مع البيانات الصغيرة وتساعد على تسريع الأداء.
الترتيب بالاختيار (Selection Sort)
في هذه الحالة، تُقسم البيانات إلى قسمين: قسم مرتب وقسم غير مرتب. تعمل الخوارزمية على أخذ البيانات غير المرتبة، والعثور على أصغر عنصر فيها، ثم نقله إلى القسم المرتب. تتكرر هذه العملية بشكل متسلسل حتى يتم ترتيب القائمة بالكامل بطريقة تصاعدية.
تُستخدم أيضًا مع البيانات الصغيرة وفعالة في تلك الحالات.
الترتيب الفقاعي (Bubble Sort)
تستخدم هذه الخوارزمية عندما لا تكون لدينا معلومات دقيقة حول حالة البيانات إن كانت مرتبة أم لا. ففي البداية تقوم بفحص جميع العناصر الموجودة في القائمة، وإذا كانت غير مرتبة، تقوم بتصنيفها. وتستمر هذه العملية حتى تصبح جميع العناصر مرتبة تمامًا.
مثال: إذا كنت تريد ترتيب سلسلة من الأرقام العشوائية بترتيب تصاعدي، فإن الخوارزمية تقوم بفحص السلسلة عدة مرات حتى تصل إلى الترتيب المطلوب. يمكن استخدامها أيضًا مع البيانات الكبيرة، لكن لا يُنصح بها لأنها عملية بطيئة نسبيًا.
الترتيب السريع (Quick Sort)
تعرف هذه الخوارزمية أيضًا باسم “التفكيك والتركيز”. فهي تقسم البيانات إلى أجزاء أصغر لمساعدتها في حل مشكلة الترتيب. في هذه الحالة، يتم اختيار عنصر واحد ليكون العنصر المحوري (Pivot)، ويتم ترتيب باقي العناصر بناءً عليه.
أي أن العناصر الأصغر من العنصر المحوري توضع قبله، والعناصر الأكبر منه توضع بعده.
الترتيب بالدمج (Merge Sort)
هي أيضًا نوع من خوارزميات “التفكيك والتركيز”، حيث تقسم كل مجموعة بيانات إلى جزأين باستمرار. وتستمر هذه العملية حتى تحتوي كل قائمة فرعية على عنصرين أو عنصر واحد فقط. وبعد أن تُرتّب هذه القوائم الفرعية حسب الترتيب المطلوب، تُدمج مع بعضها البعض لتشكيل القائمة النهائية المرتبة.
2. خوارزميات البحث (Searching Algorithms)
البحث من أبسط العمليات في مجال تكنولوجيا المعلومات، لكن تنفيذه الصحيح له أهمية كبيرة في البرمجة. تشمل هذه الخوارزميات البحث داخل قواعد البيانات الداخلية أو في المساحات الافتراضية لإيجاد المعلومات المطلوبة. عمومًا، هناك طريقتان رئيسيتان لتنفيذ عملية البحث، وهما:
البحث الخطي (Linear Search)
هي خوارزمية بسيطة جدًا وتستخدم للعثور على عنصر أو معلومة محددة ضمن مجموعة غير مرتبة. تعتمد هذه الخوارزمية على آلية البحث المتسلسل.
مثال: إذا كنت بحاجة إلى استرجاع رقم هاتف من قاعدة بيانات ضخمة تحتوي على أسماء أشخاص عشوائية، فإن خوارزمية البحث الخطي تتحقق من كل عنصر تلو الآخر حتى تجد ما تبحث عنه.
البحث الثنائي (Binary Search)
تعتمد هذه الخوارزمية على منهجية مختلفة تمامًا. فهي تبحث في هيكل البيانات باستخدام تقسيمات متتالية، وليس بالتتابع كما في السابق. تكون هذه الطريقة أكثر كفاءة إذا كانت البيانات مرتبة مسبقًا، لأنها لا تحتاج إلى مسح كامل القائمة.
مثال: في سلسلة طويلة من الأرقام التصاعدية، يبدأ البحث من العنصر الأوسط. إذا لم يكن هو العنصر المطلوب:
- وإذا كان العنصر الأوسط أصغر من المطلوب، فإن البحث يستمر في النصف العلوي.
- وإذا كان أكبر، فإن البحث يتجه إلى النصف السفلي.
تُكرر هذه العملية حتى يتم العثور على العنصر أو انتهاء القائمة، وفي هذه الحالة يُفهم أن العنصر غير موجود.
3. خوارزمية التجزئة (Hashing Algorithm)
تعتبر خوارزمية التجزئة واحدة من الخوارزميات الشائعة جدًا في إدارة هيكل البيانات، وتتميز بمستوى عالٍ من الأمان وكفاءة عالية في التعامل مع البيانات الضخمة.
تعمل خوارزمية التجزئة (Hashing) على تحويل بيانات ذات طول عشوائي إلى قيمة ثابتة ومحددة مسبقًا تُعرف بـ “قيمة التجزئة” (Hash Value). وبهذا توفر ملخصًا أو بصمة للبيانات الأصلية. من أشهر الاستخدامات لجداول التجزئة هي تشفير المفاتيح أو الرسائل.
4. الخوارزمية العشوائية (Randomized Algorithm)
جزء من منطق هذه الخوارزمية البرمجية يعتمد على العشوائية. تُستخدم الخوارزمية العشوائية عادةً مع كميات كبيرة من البيانات التي يكون من الصعب معالجتها بشكل دقيق وسريع باستخدام الطرق التقليدية.
يمكن أن يلعب العنصر العشوائي دورًا في تقليل الوقت المطلوب للعثور على الحل الصحيح، أو في تحديد احتمال صحة نتيجة معينة بعد تنفيذ الخوارزمية خلال فترة زمنية محددة.
خاتمة
لا يمكن المبالغة في أهمية خوارزميات البرمجة في التكنولوجيا الحديثة. فهي العمود الفقري لكل برنامج، والأساس الذي يُبنى عليه كل تطبيق ذكي، وكل نظام ذي كفاءة عالية. من خلال تحويل الأفكار إلى تعليمات منطقية دقيقة، تمكن الخوارزميات المبرمجين من بناء حلول ذكية لمشاكل معقدة، وتحويل البيانات الخام إلى معلومات ذات قيمة.
مع تطور التكنولوجيا وتزايد التحديات، لم يعد تصميم خوارزميات فعالة مجرد خيار، بل أصبح ضرورة لا غنى عنها لتحقيق الأداء الأمثل، وتوفير الوقت والموارد. سواء كنت مبتدئًا في عالم البرمجة أو مطورًا محترفًا، فإن فهم الخوارزميات وتطبيقاتها هو مفتاح الابتكار والتفوق في هذا عصر التحول الرقمي.
باختصار، الخوارزميات ليست فقط أداة للبرمجة — هي لغة الحواسيب، وقلب الذكاء الاصطناعي، ومستقبل التكنولوجيا.

